雨上がりのクモの巣のお話

梅雨の時期、雨が降り続く毎日を憂鬱(ゆううつ)に思う人も少なくはないでしょう。
しかしこの憂鬱な雨も、太陽に照らされて輝くことができます。
雨上がりに外に出て、クモの巣についた雨粒に見とれてしまった経験がありませんか?
いつもは厄介(やっかい)なクモの巣や雨が、そこでは驚くようなアートを作り出しています。
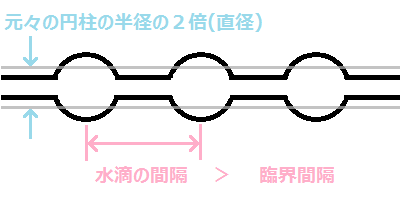
クモの巣につく水滴(すいてき)は、ぽつんぽつんとしばしば同じくらいの間隔で、糸の上に並んでいます。
雨上がりのクモの巣が美しいのは、やはりこのようにある間隔で水滴がきれいに並んでいるからでしょう。
しかし、雨のあとすぐは糸全体にべったりついていた水が、巣の主を含め
誰の手も介さずに自然とこのようにきれいに並ぶのは、いったいなぜなのでしょうか。
臨界間隔
水を形作っている小さな粒(分子)はお互いに引っ張り合っており、それにより、水にはその表面積を小さくしようとする効果(表面張力)が現れます。
この効果により、理想的には元々 糸に円柱の形でべったり張り付いていたと考えられる雨水は全体の表面積が小さくなるように形を変えていきます。
同じ体積で最も表面積が小さい形はなんでしょうか。
それは球であることが知られています。
こうして、糸の上にたくさんの水滴ができていく理由がなんとなくわかると思います。
ただし糸の上の水の全体積は決まっているのでできる水滴の間隔がせますぎると、水滴の数は増えてしまいます。
こうすると、この数の分の表面積が、球になって小さくなる分を上回り
最初の、べったり円柱状に張り付いていた水よりも全体の表面積が増えてしまうことになります。
このような状態は不安定で、普通にはおこりません。
水滴がある一定以上の間隔になって初めて、全体の表面積は元よりも小さくなります。
このような状態が安定になるため、クモの糸の上にみられる水滴は、ある一定の「臨界間隔」以上できれいに並んでしまうというわけです。
表面積だけを考えるこの理論では、水滴の臨界間隔は、元々円柱状に考えていたときの円柱半径の4.5倍と計算されます。
この美しい芸術に、昔から多くの物理学者が挑戦してきたようです。
糸の上の水の安定性にほかの効果(圧力差など)を考えることでベルギーの物理学者プラトーは臨界間隔がもっと長いこと(元々の半径の2π倍になること)を初めて示しました。
この問題に終止符を打ったのはノーベル物理学賞受賞者であるレイリー卿で彼の理論では臨界間隔は元々の半径の9.02倍です。
まとめ
もちろん、正確な値がわからなくても、おおよその原理は理解できますし
その美しさは揺るがないのも事実です。
じめじめして億劫(おっくう)でも、外に出てみればこうした現象に魅せられることもあるでしょう。
そんな時、この基本的な物理法則の偶然の積み重ねを、自然からのプレゼントだと思えば少しだけさわやかな気分になれるかもしれません。
クモの巣写真: Wikimediaより引用 (CC BY-AS 3.0) Luc Viatour / www.Lucnix.be
具体的数値の出典(計算過程もこちらに載っています): 『楽しめる物理問題200選』
(著 Peter Gn¨adig, Ken Riley, Gyula Honyek; 邦訳 近重悠一, 加藤正昭, 伊藤郁夫; 朝倉書店; 2003)
このお話は、2012/06に CAST@NET で配信されました
