円周率えんしゅうりつってなに？

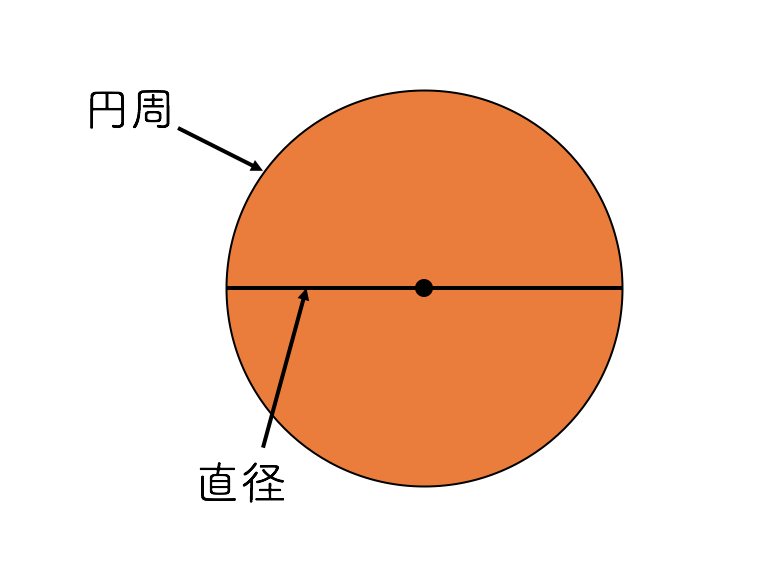
円周率えんしゅうりつとは、円の周りの長さ(円周えんしゅうといいます)が円の直径ちょっけいに対してどのくらいの大きさかを表す数字で、ふつうπパイという記号きごうで表されます。

円周率えんしゅうりつは、全ての円に対して同じ値あたいになることがわかっていて、円周率えんしゅうりつ = 3.141592653...です。

円周えんしゅうは直径ちょっけい×円周率えんしゅうりつで計算できるので、直径ちょっけいが1cmの円の円周えんしゅうは約3.14cmになることがわかります。

どうして点を打うつだけで円周率えんしゅうりつが求もとまるの？

正方形の中にランダムに点を打うったとき、ある図形ずけいの中に点が入る割合わりあいを考えてみましょう。感覚的かんかくてきには狭せまい図形ずけいの中には入りづらく、広い図形ずけいだと楽に入りそうです。

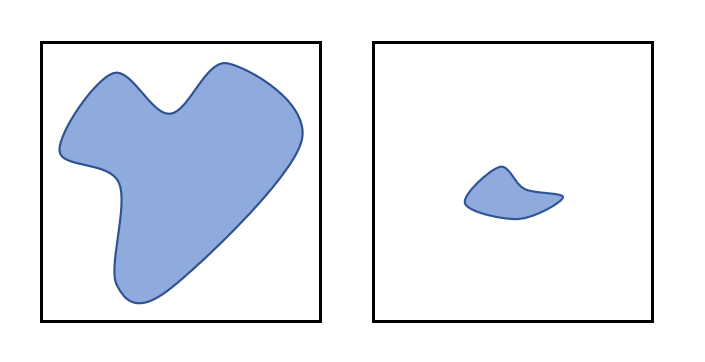
実はこの割合わりあいは点の打うち方がしっかりとランダムであれば、正方形の面積めんせきと図形ずけいの面積めんせきの比にだんだんと近づいていきます。

正方形の1辺の長さを2cmとすると正方形の面積めんせきは 2cm×2cm=4cm² 、半径はんけい1cmの円の面積めんせきは (円周率えんしゅうりつ) ×1cm×1cm＝(円周率えんしゅうりつ) cm² です(6年生の算数で習います)。よって打うった点の数、円の中に入った点の数を数えることで、次のように円周率えんしゅうりつのだいたいの値を計算することができるというわけなのです。

モンテカルロ法で円周率えんしゅうりつを求もとめよう

今回の進捗しんちょく企画きかくでは「モンテカルロ法」という手法しゅほうを用いて円周率えんしゅうりつの近似値きんじちを求もとめました。モンテカルロ法とは、ランダムな数字「乱数らんすう」を利用して、シミュレーションや数値すうち計算を行う手法しゅほうのことです。

今回は円に直接ちょくせつ、点をランダムに打うって、円周率えんしゅうりつの近似値きんじちを求もとめましたが、実は円を使わずに円周率えんしゅうりつの近似値きんじちを求もとめる方法があります。その方法を説明したいと思います。

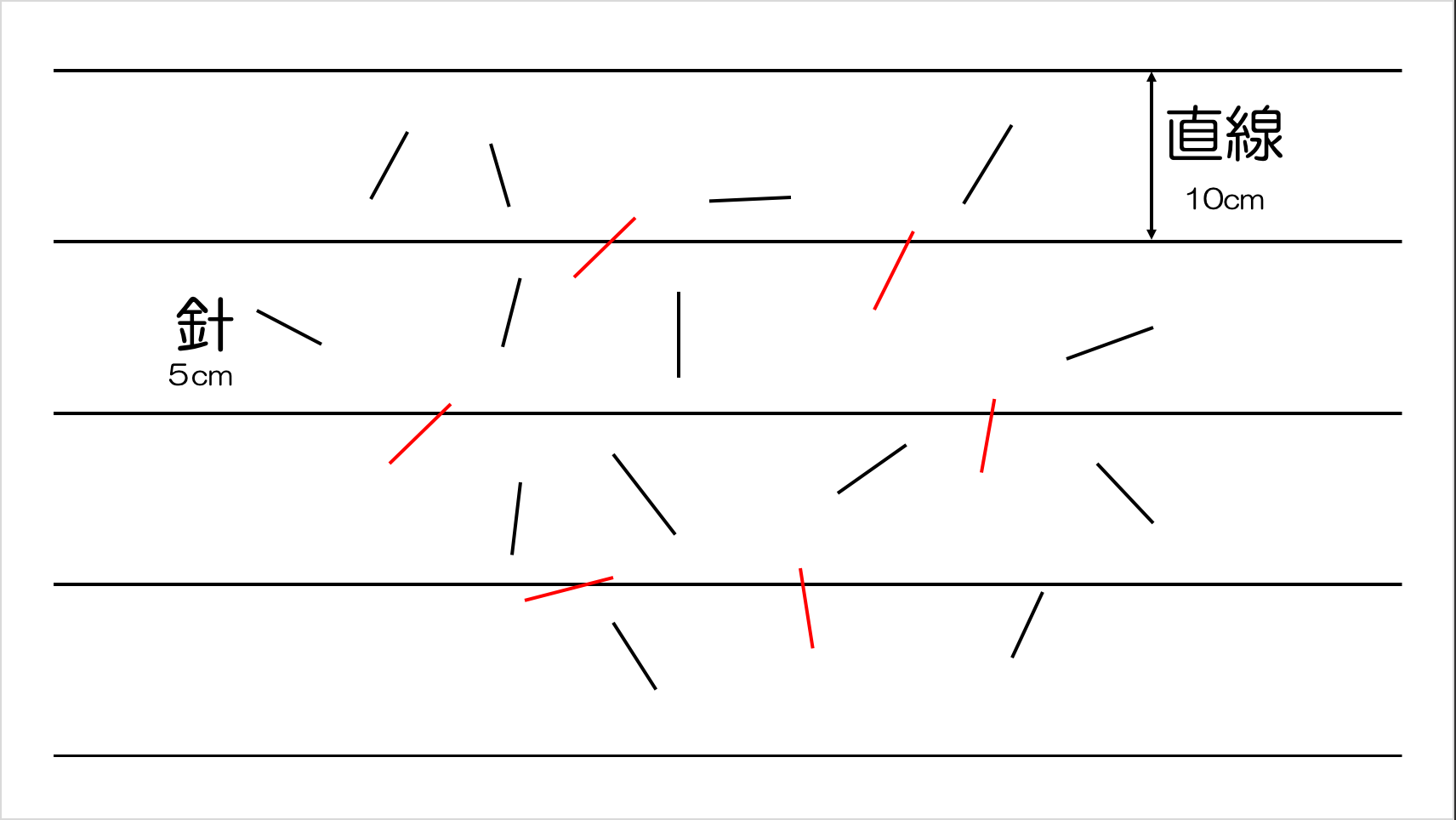
使うものは、針はり、紙、ペンです。

まず上の図のように、紙に10cm間隔かんかくで平行線をたくさん引いて、長さ5cmの針はりを好きな位置いちから紙に落としていきます。このとき、紙に落ちた針はりのうち、平行線と交わっているものの本数を数えていくことにします。

本当は、平行線の間隔かんかくや針はりの長さは自由に決められるのですが、今回はイメージがしやすいように、平行線の間隔かんかくを10cm，針はりの長さを5cmと決めてしまいます。

これを繰くり返すと、このとき実はの値が円周率えんしゅうりつに収束しゅうそくしていくのです。

なぜこのような方法で円周率えんしゅうりつが求もとまるのか、実はこの方法の背景はいけいには「ビュフォンの針はり」という有名な確率かくりつの問題があります。

きちんと理解りかいするには、高校、大学で習う確率かくりつや積分せきぶんに関する知識ちしきが必要なため、説明は割愛かつあいしますが、興味きょうみのある人はぜひ調べてみてください。

この方法も「針はりをランダムに落とす」ということからモンテカルロ法の応用おうよう例の一つです。

針はりを落とすだけで円周率えんしゅうりつが求もとまるなんて不思議ふしぎですね。針はりの代わりに爪楊枝つまようじなどを使っても再現できるので、お家でもぜひ試してみてほしいと思います。