このゲームでは、相手と交互(こうご)に石をとっていきます。「最後(さいご)の石をとった方が勝(か)ち」という一見運(うん)任(まか)せのゲームのようですが、実は数学の考え方を使うことで勝(か)つことができるんです！何度も遊(あそ)びながら、必勝(ひっしょう)法(ほう)を探(さが)してみましょう！

※ゲームの読み込(こ)みに時間がかかる場合(ばあい)がありますがそのままお待ちください。

ヒント

1. このゲームには必勝法ひっしょうほうがあるよ！自分の順番じゅんばんが終わったときに、皿の上の石の数がどのようになっていればよいかに注目ちゅうもくして考えてみよう！
2. 必勝法ひっしょうほうには、「二進法しんほう」というものが関わっているよ。石の数を「二進法しんほう」で表して考えると何か法則性ほうそくせいが見えてくるかも？

解説かいせつ

難易度なんいど：ふつう（皿が二つ）のとき

自分の順番じゅんばんが終わるときに、二つの皿にある石の数が同じになるようにしよう。二回目以降の自分の番では、相手と同じ石の取り方をすると考えてもよいでしょう。例えば、二つの皿の石の数が同じときに、相手が右の皿から2個石を取ったら、その次の自分の番では左の皿から2個石を取れば、二つの皿の石の数はまた同じになりますよね。

それを繰くり返せば、最後には両方の皿の石の数が同じ0となって勝てるはず！

難易度なんいど：むずかしい/とてもむずかしい（皿が三つ）のとき

この必勝法ひっしょうほうでは「二進法しんほう」というものがポイントになっているよ！

二進法しんほうとは

ここでは、数の数え方の話をします。私たちは普段、0から9までの数字を使って数を数えていますよね。1, 2, 3,…と数えていって、9の次は位が上がって10になります。同じように、10, 11, 12,…,20,…30,…と数えていって、99の次はまた位が上がって100になります。このことを、次のように言うことができます。すなわち、「10個集まると位が上がる」ということです。1が10個集まって10に、10が10個集まって100に、100が10個集まって1000に…というふうに位が上がっていきますよね。私たちが普段ふだん使っているこの数の数え方のことを、「十進法しんほう」といいます。

二進法しんほうとは、この数の数え方の一つです。二進法しんほうでは、上で説明した十進法しんほうの「10」を「2」に変えればよいのです。つまり、「2個集まると位が上がる」ということです。十進法しんほうでは0から9までの数字を使いましたが、二進法しんほうでは0と1の二つしか使いません。二進法しんほうでは１はそのまま1ですが、2は「10」と表されます。なぜなら「2個集まると位が上がる」からです。3はそれに1を足して「11」であり、4は「2が2個集まった」ので位が上がり、「100」となります。

十進法しんほうと二進法しんほうの対応たいおうを表に整理せいりしてみましょう。

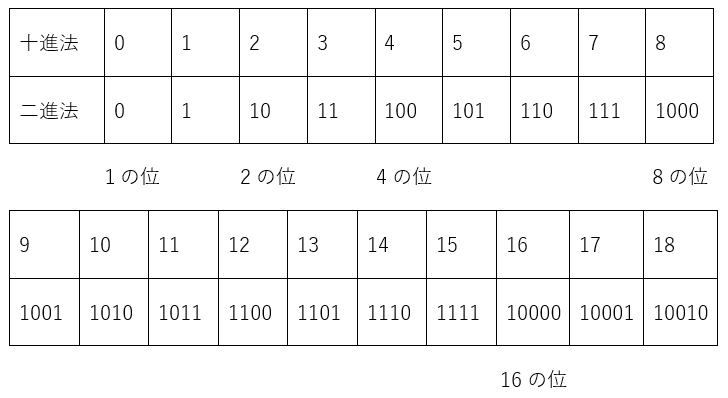
では、十進法しんほうで表された数を二進法しんほうに変える方法を紹介しょうかいします。

そこで使うのが、筆算です。ただし、割る数・割られる数とその答えの位置は逆にして書き、その右にあまりの数を書きます。（割り切れたときは0と書きましょう。）

十進法しんほうの数字を2で割り続け、答えが0か1になったら終了です。最後の答え→その計算のあまり→その一つ前のあまり という順番じゅんばんで数字を並べていくと、それが二進法しんほうで表された数になっています。

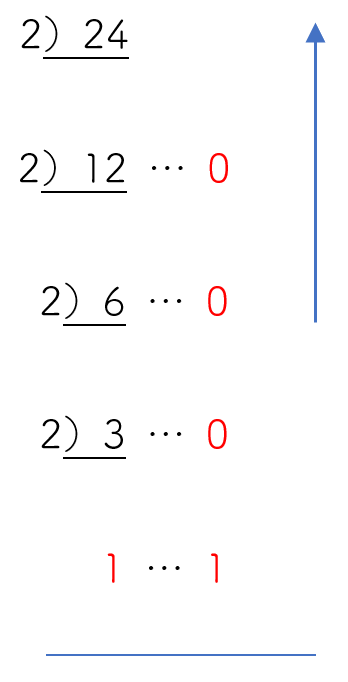
24は二進法しんほうで表すと確かに11000になっています。

それでは、この二進法しんほうをどのように使うと必勝法ひっしょうほうになるのでしょうか。

まずは、それぞれの皿に乗っている石の数を二進数しんすうに変えてみましょう。

左の皿の石の数は8個なので、

というふうに計算すると、8は1000と表されることがわかりますね。

真ん中の皿の石の数は9個です。同じように筆算をしてもいいですが、ここでは8に１を足すと考えるほうが楽でしょう。1000の最後に1を足して、1001となります。

右の皿の石の数は10個です。こちらも9に1を足すと考えます。1001の最後に1を足すと、「1が2個集まる」ので位が上がり、1010となります。

次に、こうして二進法しんほうで表した数を使って、各桁かくけたの数を足しましょう

上の例で、三つの皿の上にある石の数8、9、10は二進法しんほうでそれぞれ1000、1001、1010と表されることを見てきました。この三つの数を足します。

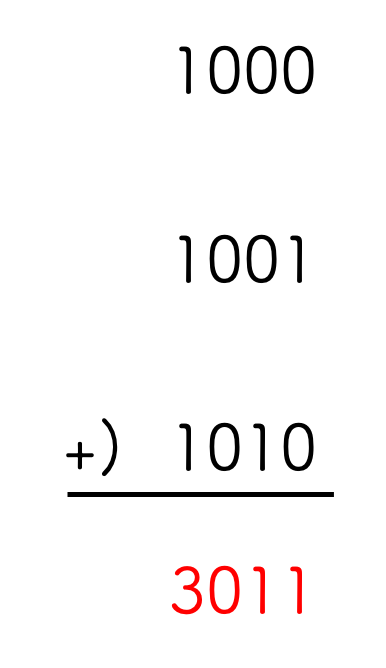
では、このゲームに勝つためには、どの山からいくつ石を取ったらいいのでしょうか。

必勝法ひっしょうほうは、自分の順番じゅんばんの終わりに、こうして計算した数の「各桁かくけたの数が全て偶数ぐうすう」になるように石を取ることです。

例）3、0、1、1を全て偶数ぐうすうにするには、例えば3と1を2にすればいいですね。そのためには、例えば1000を0011にすればよいでしょう。

0011+1001+1010 = 2022 (2も0も偶数ぐうすうですね)

つまり、石が8（=1000）個乗っている皿から5個取って3（=0011）個にすればよいのです

「各皿の石の数の和を全て偶数にすること」を繰り返していくと、あら不思議ふしぎ、ゲームに勝つことができます！手元で計算しながら、頑張って勝てるまで挑戦ちょうせんしてみてください！

どうしてこの方法で勝つことができるのかは、数学の証明問題しょうめいもんだいです。気になった人は調べてみたり、自分で証明しょうめいに挑戦ちょうせんしてみたりすると面白いかもしれません！