バイオミメティクスブースの動画では、周りの⻑さが等しい正三⾓形・正⽅形・正六⾓形のうち、⼀番⼤きいのは正六⾓形になる、ということを紹介しました。ここでは、本当に正六⾓形が⼀番⼤きいのかをたしかめてみたいと思います!
初めに、周りの⻑さの等しい正三⾓形・正⽅形・正六⾓形を準備します。
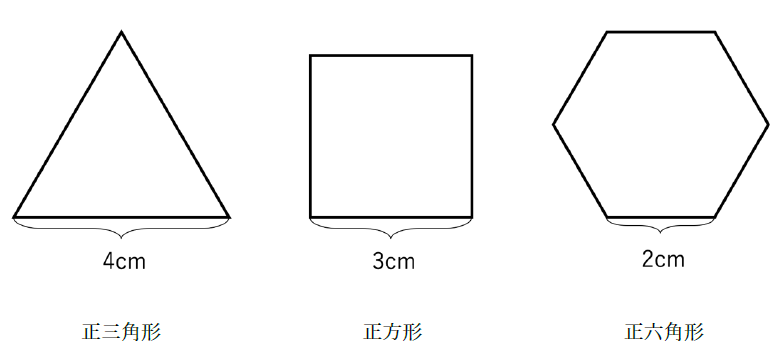
正三⾓形は一辺が4cm、正⽅形は一辺が3cm、正六⾓形は一辺が2cmです。こうすれば、どれも周の⻑さは12cmで同じになりますね。少し難しい算数を使って、これらの面積(広さ)を正確な値として求めることもできますが、今回はより多くのみんなに分かってもらえるよう、分かりやすいやり⽅で⼤きさを⽐べていこうと思います。
正三⾓形と正六⾓形
正三⾓形と正六⾓形の⼤きさを比べるにはどうしたら良いでしょうか?そのまま重ねても重なる部分とはみ出てしまう部分があってうまく比べられません。そこでここでは、正三⾓形も正六⾓形も「⼩さな正三⾓形に分けられる」ということを使って⽐べてみます。
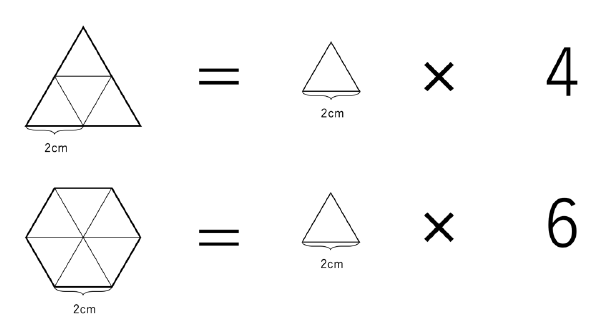
上の図のように、⼀辺が2cmの正三⾓形に分けてみます。すると、正三⾓形は4つ分、正六⾓形は6つ分になっていることがわかります。同じカタチが4つ集まったものと、6つ集まったものとでは、6つ集まったものの⽅が⼤きいのは明らかですね。というわけで、正三⾓形よりも正六⾓形の⽅が⼤きいことが示せました!
正⽅形と正六⾓形
次に、正⽅形と正六⾓形を比べてみましょう。今度は正⽅形を正三⾓形に分けることはできないので、先ほどとは別の工夫が必要になります。そこで、ここでは下の図のように、正六⾓形の形を変えることで⼤きさを⽐べてみたいと思います。
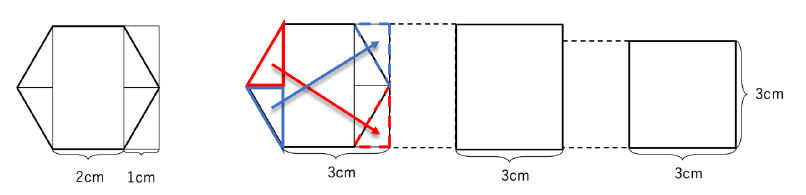
図を⾒ただけでは分かりにくいと思うので、以下でくわしく説明していきます。⼀番左の図を⾒てください。先ほどは正三⾓形に分けた正六⾓形ですが、ここでは図のように、真ん中に⼤きめの四⾓形、そしてその周りに4つの三⾓形、と分けてみます。
⼀つ右の図に進んで、左側にあった⼆つの三⾓形(⾚と⻘)を、それぞれ対応する点線で示した場所にもっていきます。すると、底辺が3cm で、正六⾓形と同じ⾼さの⻑⽅形(右から2番目の図)ができました!⼀部分を切って動かしただけなので、この⻑⽅形も、もとの正六⾓形と同じ⼤きさです。⼀番右の図は正⽅形ですが、こちらも底辺が3cm だったので、より⾼さの⾼い、正六⾓形から作った⻑⽅形の⽅が⼤きいことが分かりますね!少し遠回りだったかもしれませんが、正⽅形より正六⾓形の⽅が⼤きいことが示せました!
さて、ここまでで、「正三⾓形より正六⾓形が⼤きい」こと、「正⽅形より正六⾓形が⼤きい」ことが分かりました。つまり、正三⾓形・正⽅形・正六⾓形の3つの中では、正六⾓形が⼀番⼤きいことが無事たしかめられました!ところで、周りの⻑さが同じカタチの中で、⼀番⼤きいのはどんなカタチでしょうか?わっかになったひもを机の上において、ひもの内側が⼀番⼤きくなるようにカタチを変えてみると考えやすいかもしれません。答えは、「円」です。ひもであれば、きれいな丸のカタチになるようにした時に、⼀番⼤きくなります。考えてみれば、正三⾓形・正⽅形・正六⾓形のうち、⼀番⼤きかった正六⾓形は、3つの中では⼀番円に似たカタチだと⾔えますね。また、同じ周の⻑さをもつ正○⾓形どうしの⼤きさを⽐べると、より多くの⾓をもつ(つまり、○に⼊る数字が⼤きい)ものほど面積(広さ)は⼤きくなります。
それでは、なぜ今回の実験では円や他の正○⾓形は使わず、正三⾓形、正⽅形(正四⾓形)、正六⾓形の3つだけで⽐べたのでしょうか?それは、円や正○⾓形の中で、蜂の巣のようにしきつめて構造を作れるのはこの3つだけだからです。円や正五⾓形などでは、しきつめようとしてもすき間ができてしまい、うまく構造を作ることができません。同じカタチをしきつめたものを「平面充填」と⾔いますが、実は平面充填は正三⾓形、正⽅形、正六⾓形以外にも存在します。(「千鳥格子」などがその例です。⾒たことがない⼈は調べてみてくださいね!)
今回は3つだけを比べましたが、正六⾓形は、それらの平面充填のできるすべての図形の中で、周の⻑さに対する面積(広さ)が最大と知られています。蜂の巣のカタチ、ハニカム構造の不思議さ、すごさをさらに実感してもらえたでしょうか?興味のある⼈は、面積を比べるの別⽅法や、正○⾓形の平面充填が3つだけに限られる理由など、⾃分で考えてみるといろいろな発見があって面白いかもしれません!
コラムに関連した企画
CASTのメールマガジン「CAST@NET」
「CAST@NET」毎月第一土曜日に配信している東大CASTのメールマガジン「CAST@NET」では、東大CASTのイベント情報等に加え、科学コラムを配信しています。東大CASTのホームページから、ぜひご登録ください!


